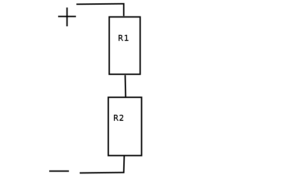
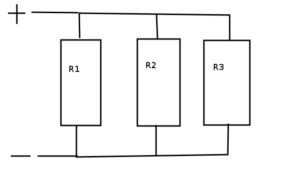
When most people hear the word power they probably think of this:
Or they might think of the idea of “energy”, but energy and power are actually two different things. Energy is defined as the ability to do “work” which in physics is a force that is done over a distance that is parallel to the force.
Basically: energy is the ability to do stuff. Power is the rate at which energy is transferred from one thing to another. Energy is measured in Joules, and power is measured in watts, and one watt is equal to one Joule being transferred per second.
This is relevant to electronics because electrical devices like light-bulbs have a rating telling you how much POWER it uses. A light-bulb that is left on overnight will use more energy than one that is left on for an hour, so the light-bulb manufacturers tell you how much power it will use, and let you figure out how much energy it will use given how long you want it to run.
They could probably tell you how much energy it will use, but that would imply that it was engineered to burn out after using a specific amount of energy, and that would be unethical. The power companies do however keep track of how much energy you’ve used. They keep track of it not in “joules” but in kilowatt-hours. Basically one thousand watts being used for one hour which is equal to 3.6 million joules (a joule is not a lot of energy).
It’s also important to understand that the power that a circuit uses is the current going through it multiplied by the voltage across it. So in other words the electrons are losing energy as they “fall”, and the voltage (or “height”) indicates how much energy they had initially, and the current (or “rate of falling”) indicates how quickly the energy from that electron is extracted and used for whatever you were hoping to do with it.
Therefore if you have a circuit with a low resistance, and you put a high voltage across it it will start to use a lot of power. This might not always be a bad thing though. Sometimes using a lot of power can be a good thing. If I built a machine for picking up big heavy boxes then I’d like the motors to be able to be able to use a lot of power so that it can pick up the heavy box more quickly. Or maybe I have a light-bulb, and I want it to be REALLY bright, so I want one that uses a lot of power because that means it can use a lot of energy very quickly for being bright.
It’s important to understand: efficiency is what’s important. I don’t want to buy a light-bulb that uses a lot of power yet doesn’t make a lot of light (presumably it just heats up a bunch). That would be a ripoff. Unfortunately the light-bulbs that can use a lot of power without dying tend to be very inefficient, while the light-bulbs that are really efficient can’t have a lot of power going through them or they die.
This is true of not just light-bulbs but pretty much everything. Machines that are powerful enough to move mountains tend to be inefficient at doing so.