Because I didn’t understand voltage growing up I kind of rejected the idea of ohm’s law when I learned it because it didn’t make sense to me. I misunderstood voltage as being the rate that electrons flow through a wire, but apparently that’s what current is too?

Now I finally understand how it works: voltage is the “height” that the electrons are at, and current is the rate that they “fall down”. Current is measured in amps, and one amp is equal to one coulomb of charge going through the device per second.

Also pretty much everything has “electrical resistance” in addition to mass, charge, density, and those kinds of things. Whenever you put a voltage across some particular thing, the electrons will “fall down” through that material, and the rate of falling is the called the current.

The object that the current is going through is sort of like the atmosphere of a planet, I guess. It slows things down. Resistance is kind of like the thickness of that atmosphere. So when a voltage is placed across something, a current will pass through it, and the following formula will apply:

[math]$\begin{math}E=I*R$[/math]

where E is the voltage (short for “electromotive force” because obviously), I is the current, And R is the resistance. Many people get confused about the cause and effect here: “So putting a voltage across something causes the current to happen afterwards?” You might be saying to yourself, out loud, in a room full of people.

Try not to think of it as so much “cause and effect” but more as “any time there is a voltage across a resistance there will be a current, and any time there is a current going through a resistance there will be a voltage, and any time there’s a current traveling across a voltage there will be a resistance between the two”.

Basically the current and the voltage happen pretty much simultaneously. To fully understand this try playing around with the math to see how all of this works out with different resistances, currents, and voltages.

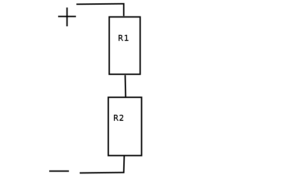
Here are a few handy things to keep in mind: if you have some kind of hypothetical electrical device that is supposed to have a resistance (like some kind of “resistor”) then placing two of them in series doubles the amount of resistor that the electrons have to fall through, and therefore doubles the resistance. The resistances add up when the are put “in series” like this:

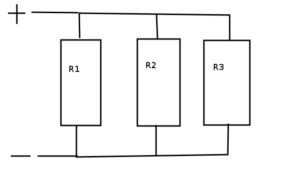
Meanwhile putting them side by side with each other will cut the resistance in half because if the voltage across them is the same, then they each have the same amount of current going through each of them. This means that all together they have twice as much current going through this whole circuit than if there was only one of these things. Twice the current with the same voltage means half the resistance if you do the math.

For any number of resistors “in parallel” like this the following rule will apply:

[math]$\Huge \begin{math}R=\frac{1}{\frac {1} {R1} + \frac {1} {R2} + \frac {1} {R3} + …}$[/math]

R is the total resistance of the circuit, and R1, R2, R3, and so forth are the resistors in parallel.
This means that as you add more resistors in parallel the resistance of the entire thing goes down. Adding something with a big resistance in parallel causes it to go down less than putting something with almost no resistance in parallel because math.

This is important because it means that although a single circuit (like just one resistor) might have a big resistance, and therefore not use much current, it can still be a part of a much bigger circuit that has a lot of parts, and therefore, as a whole, has very little resistance and uses a lot of current.

So in other words all circuit have a resistance, and will have a current going through them when a voltage is placed across them, and the same is true for any circuit that this circuit is made of.

Note that the resistance that a circuit has can change, and so can the current going through it, and the voltage across it; however ohm’s law will always be true for that circuit no matter what the situation.